How MAD is Calculated for Forecast Error Measurement

Executive Summary

• MAD is a universally accepted forecast error measurement.
• MAD is generally low in effectiveness in providing feedback to improve the forecast.

Introduction

MAD, or Mean Absolute Deviation, is one of the most common forecast error measurements in use. MAD is moderately easy to understand and relatively easy to calculate. However, when MAD is used, in most cases, the problems with MAD are not explained to the audience, which is an issue that also generalizes to the other primary forecast error measurement calculations. At Brightwork, we do not use MAD when we perform forecast analysis. In this article, you will learn about the issues with MAD that reduce a person or company’s ability to improve their forecast accuracy.

Our References for This Article

To see our references for this article and other related Brightwork articles, visit this link.

How MAD is Calculated

How MAD is calculated is one of the most common questions we get.

MAD is calculated as follows.

1. Find the mean of the actuals.
2. Subtract the mean of the actuals from the forecast and use the absolute value.
3. Add all of the errors together.
4. Divide by the number of data points.

The formula is..

MA = Mean of Actuals

= SUM(ABS(F – MA))/# of Data Points

The Broader Context of How MAD is Calculated

Like MAPE, MAD uses absolute values, so one does not understand the bias. But because MAD is squared, the error is not proportional — meaning that larger errors become much more significant as they are squared. Any error measurement that is not proportional makes it intuitively more difficult to understand than a proportional measure. How is a non-forecasting-focused person supposed to interpret non-proportional forecast errors? Our brain is designed to understand proportionality.

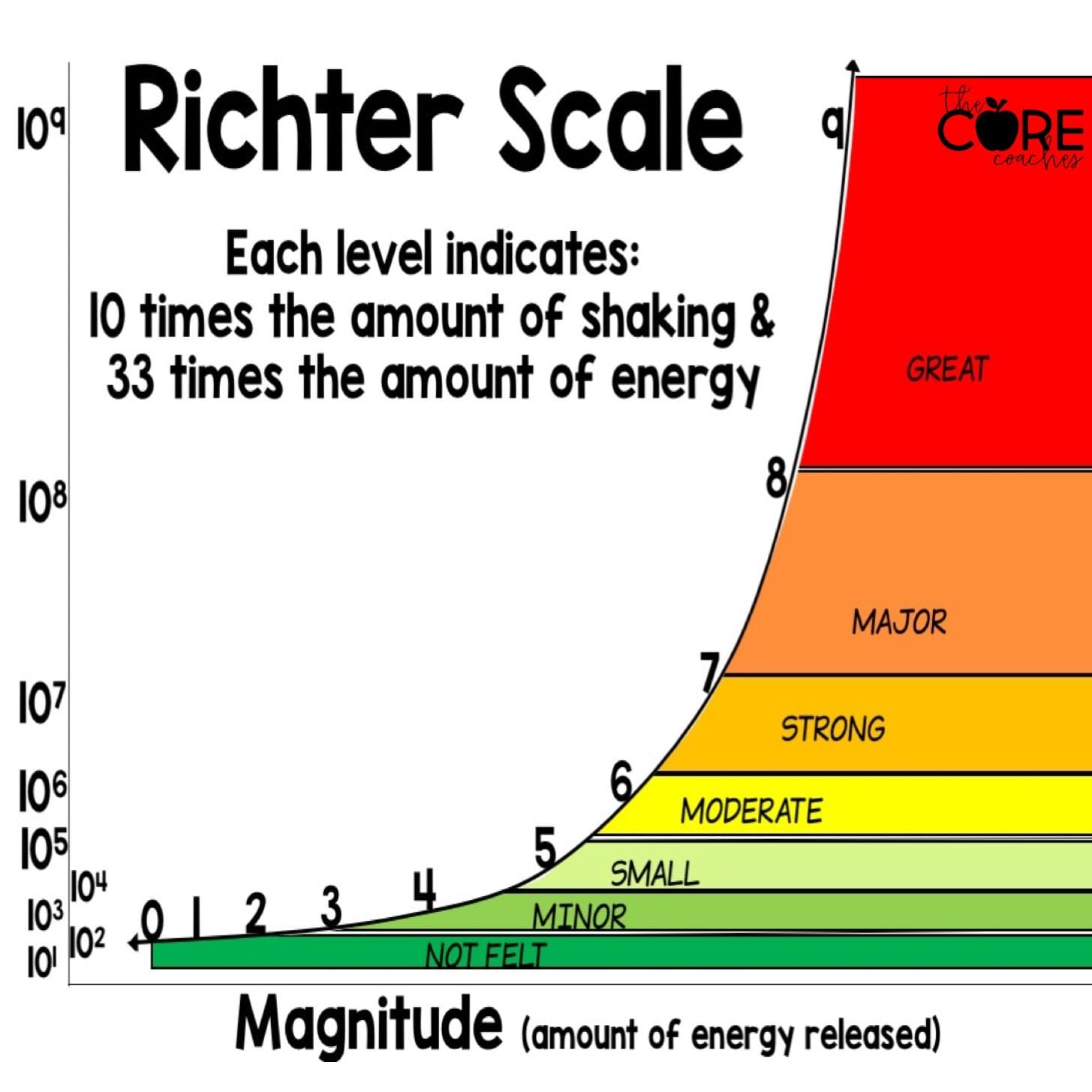
For example, the Richter Scale is a logarithmic scale, which allows a relatively small number of values to represent large magnitudes in difference. However, it also means humans cannot calculate the difference between different earthquake values.

The Same Problem With All the Standard Forecast Error Measurements

How MAD is calculated is one of the most common questions we get. However, the narrow question broadens when one looks at the different dimensions of forecast error.

Due to its lack of proportionality, MAD was never a forecast error method before developing our own. However, in addition to this lack of proportionality, MAD shares the same problems with all standard forecast error measurements.

These include the following:

1. They are difficult to weigh. Any forecast error aggregated beyond the product location combination must be weighed to make any sense.
2. They make comparisons between different forecasting methods overly complicated.
3. They lack the context of the volume of the demand history or the price of the forecasted product, meaning that the forecast errors must be provided with context through another formula.
4. They are difficult to explain, making them less intuitive than a different approach.